Question

Find the lengths of the sides of the triangle PQR. P(2, −3, −4), Q(8, 0, 2), R(11, −6, −4) |PQ| = Incorrect: Your answer is incorrect. |QR| = |RP| = Is it a right triangle? Yes No Is it an isosceles triangle? Yes No

Answer 1

the length PQ is 9 units,the length QR is 9 units,the length PR is 9.48 units,the triangle is not a right triangle,this is a isosceles triangle

Explanation:

Hello, I think I can help you with this

If you know two points, the distance between then its given by:

`P1(x_(1),y_(1),z_(1) ) \\P2(x_(2),y_(2),z_(2))\\\\d=\sqrt{(x_(2)-x_(1) )^(2) +(y_(2)-y_(1)  )^(2)+(z_(2)-z_(1) )^(2) }`

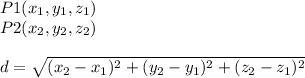
Step 1

use the formula to find the length PQ

Let

P1=P=P(2, −3, −4)

P2=Q=Q(8, 0, 2)

`d=\sqrt{(8-2)^(2) +(0-(-3))^(2)+(2-(-4))^(2)} \\ d=\sqrt{(6)^(2) +(3)^(2)+(6 )^(2)}} \\d=√(36+9+36)\\d=√(81) \\d=9\\`

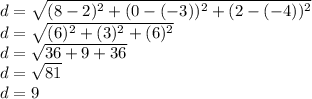
the length PQ is 9 units

Step 2

use the formula to find the length QR

Let

P1=Q=Q(8, 0, 2)

P2=R= R(11, −6, −4)

`d=\sqrt{(11-8)^(2) +(6-0))^(2)+(-4-2 )^(2)}  \\\\\\d=\sqrt{(3)^(2) +(6)^(2)+(-6 )^(2)}} \\d=√(9+36+36)\\d=√(81) \\d=9\\`

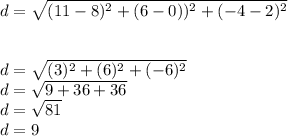
the length QR is 9 units

Step 3

use the formula to find the length PR

Let

P1=P(2, −3, −4)

P2=R= R(11, −6, −4)

`d=\sqrt{(11-2)^(2) +(-6-(-3)))^(2)+(-4-4 )^(2)}  \\\\\\d=\sqrt{(9)^(2) +(-6+3)^(2)+(-4-(-4) )^(2)}} \\d=√(81+9+0)\\d=√(90) \\d=9.48\\`

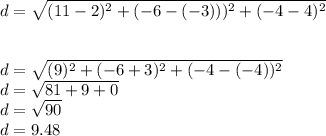
the length PR is 9.48 units

Step 4

is it a right triangle?

you can check this by using:

`side^(2) +side^(2)=hypotenuse ^(2)`

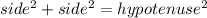
Let

side 1=side 2= 9

hypotenuse = 9.48

Put the values into the equation

`9^(2) +9^(2) =9.48^(2)\\ 81+81=90\\162=90,false`

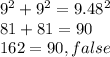
Hence, the triangle is not a right triangle

Step 5

is it an isosceles triangle?

In geometry, an isosceles triangle is a type of triangle that has two sides of equal length.

Now side PQ=QR, so this is a isosceles triangle

Have a great day