Answer: The required range of the given function is {-8, -5, 4}.
Step-by-step explanation: We are given to find the range of the following function :
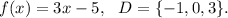
Since the domain D contains points -1, 0 and 3, so the range will be the following set :
{f(-1), f(0), f(3)}.
We have
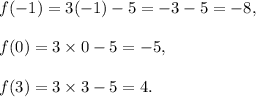
Thus, the required range of the given function is {-8, -5, 4}.