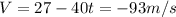Question

A ball is thrown into the air by a baby alien on a planet in the system of Alpha Centauri with a velocity of 27 ft/s. Its height in feet after t seconds is given by y = 27 t − 20 t 2 y=27t-20t2. A. Find the average velocity for the time period beginning when t=3 and lasting .01 s: Preview .005 s: Preview .002 s: Preview .001 s: Preview NOTE: For the above answers, you may have to enter 6 or 7 significant digits if you are using a calculator. Estimate the instanteneous velocity when t=3. Preview Get help: Video

Answer 1

`V_(3.01)=-93.2m/s`

`V_(3.005)=-93.1m/s`

`V_(3.002)=-93.04m/s`

`V_(3.001)=-93.02m/s`

`V_(3)=-93m/s`

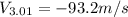
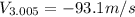
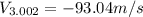
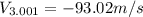
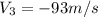
Step-by-step explanation:

To calculate average velocity we need the position for both instants t0 and t1.

Now we will proceed to calculate all the positions we need:

`Y_(3)=-99m/s`

`Y_(3.01)=-99.932m/s`

`Y_(3.005)=-99.4655m/s`

`Y_(3.002)=-99.18608m/s`

`Y_(3.001)=-99.09302m/s`

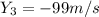
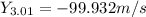
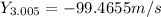
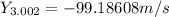
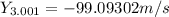
Replacing these values into the formula for average velocity:

`V_(3-3.01)=(Y_(3.01)-Y_(3))/(3.01-3)=<strong>-93.2m/s</strong>`

`V_(3-3.005)=(Y_(3.005)-Y_(3))/(3.005-3)=<strong>-93.1m/s</strong>`

`V_(3-3.002)=(Y_(3.002)-Y_(3))/(3.005-3)=<strong>-93.04m/s</strong>`

`V_(3-3.001)=(Y_(3.001)-Y_(3))/(3.001-3)=<strong>-93.02m/s</strong>`

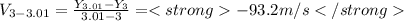
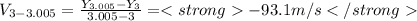
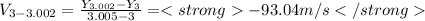
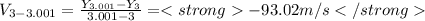
To know the actual velocity, we derive the position and we get:

`V=27-40t = -93m/s`