Question

A mass m = 550 g is hung from a spring with spring constant k = 2.8 N/m and set into oscillation at time t = 0. A second, identical mass and spring next to the first set is also set into motion. At what time t should the second system be set into motion so that the phase difference in oscillations between the two systems is pi/2?

Answer 1

The second system must be set in motion
`t=0.70s` seconds later

Step-by-step explanation:

The oscillation time, T, for a mass, m, attached to spring with Hooke's constant, k, is:

`T=2\pi\sqrt((m)/(k) )`

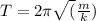
One oscillation takes T secondes, and that is equivalent to a 2π phase. Then, a difference phase of π/2=2π/4, is equivalent to a time t=T/4.

If the phase difference π/2 of the second system relative to the first oscillator. The second system must be set in motion
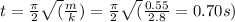`t=(\pi)/(2)\sqrt((m)/(k))=(\pi)/(2)\sqrt((0.55)/(2.8)= 0.70s)` seconds later