Answer:
The angles between the curves at the points of intersection are:
0º, 1.3º
Explanation:
The intersections points are found by setting the equations equal to each other and solving the resulting equation:
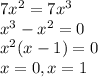
The angles of the tangent lines can be found by stating their slopes.
To find the slope we differentiate the equations:

Then we plug the x-coordinates of the intersections:
For x=0 we get the slopes are both 0:
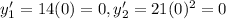
So the angles of inclination of the lines are the same their difference is 0. Hence the angle between the tangent curves is also 0º at the point of intersection at x=0
For x=1 we get the following slopes:
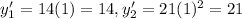
The slopes are the tangents of the angles. Therefore, to get the angle between the lines we do:
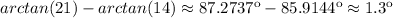
So, 1.3º is the angle between the curves at the second point of intersection at x=1.