Answer:
The probability of choosing exactly 2 male and 4 female students =

Explanation:
We are given that a class has 35 students
Number of male=16
Number of female=19
We have to choose 6 students for committee
We have to find the probability that exactly 2 male students are selected
Probability=P(E)=
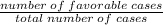
If we have to choose total 6 student in which 2 male and 4 female
Combination formula:
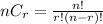
Using the formula
The probability of choosing exactly 2 male and 4 female students =
