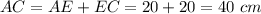Question

Lourdes is making a frame in the shape of a parallelogram. She adds diagonal braces to strengthen the frame. Parallelogram A B C D is shown. Diagonals are drawn from point A to point C and from point D to point B and intersect at point E. The length of D E is (3 y + 6) centimeters, the length of E B is (5 y minus 10) centimeters, and the length of E C is (2 y + 4) centimeters. How long is the brace that connects points B and D? 8 cm 16 cm 30 cm 60 cm

Answer 1

60cm

Explanation:

Answer 2

60 cm

Explanation:

Parallelogram ABCD is shown in attached diagram. The diagonals of the parallelogram bisect each other, so

AE = EC

BE = ED

Ib DE = 3y + 6 cm, BE = 5y - 10 cm, then

`3y+6=5y-10\\ \\3y-5y=-10-6\\ \\-2y=-16\\ \\2y=16\\ \\y=8\ cm`

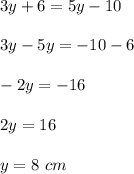
Now, EC = 2y + 4, so

`EC=2\cdot 8+4=16+4=20\ cm`

Since AE = EC, then AE = 20 cm

The brace that connects points B and D has the length

`BD=BE+ED=3y+6+5y-10=8y-4=8\cdot 8-4=64-4=60\ cm`

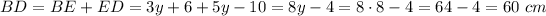
The brace that connects points A and C has the length

`AC=AE+EC=20+20=40\ cm`