Question

The following data are direct solar intensity measurements (watts/m2 ) on different days at a location in southern Spain: 562, 869, 708, 775, 775, 704, 809, 856, 655, 806, 878, 909, 918, 558, 768, 870, 918, 940, 946, 661, 820, 898, 935, 952, 957, 693, 835, 905, 939, 955, 960, 498, 653, 730, and 753. Calculate the sample mean and sample standard deviation. Prepare a dot diagram of these data. Indicate where the sample mean falls on this diagram. Give a practical interpretation of the sample mean.

Answer 1

Mean: 810.51

Standard deviation: 128.32

Explanation:

First, we calculate the sample mean. We have 35 data samples, so we compute it as
`\displaystyle (562 + .... + 753)/(35)`.

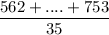In general, given a set of n samples
`\{ X_1,...,X_n\}`, we calculate the sample mean as

`\displaystyle \bar{X} = \sum_(i=1)^n (X_i)/(n)`.

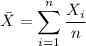For the standard deviation
`\sigma`, we first begin by calculating it's square. It can be obtained from the formula

`\displaystyle \sigma ^2 = \sum_(i=1)^(n) \frac{(X_i - \bar{X})^2}{n-1}`

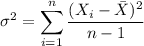
By taking square root after computing the right hand side, we attain the desired value.

The attached image shows the dot diagram of this sample. The bottom pink vertical line shows the mean, and the two horizontal pink lines have a lenght of
`\sigma`.

The standard deviation means "The average expected distance a new sample will be from the mean". That's why usually, data samples which are denser around the mean have smaller standard deviations (as opposed to distributions who have a lot of values far away from the mean, which will make the standard deviation grow bigger).