Question

Problem 6: A rocket accelerates upward from rest, due to the first stage, with a constant acceleration of a1 = 94 m/s2 for t1 = 23 s. The first stage then detaches and the second stage fires, providing a constant acceleration of a2 = 39 m/s2 for the time interval t2 = 34 s. Part (a) Enter an expression for the rocket's speed v1 at time t1 in terms of the variables provided. Part (b) Enter an expression for the rocket s speed v2 at the end of the second period of acceleration in terms of the variables provided in the problem statement Part (c) Using vow expressions for speeds v1 and v2 calculate the total distance trailed in meters, by the rocket from launch until the end of the second period of acceleration.

Answer 1

a) v1 = a1*t1 = 2162 m/s

b) v2 = v1 + a2*(t2-t1) = 2591 m/s

c)
`Dt = D1 + D2 = (v1^(2))/(2*a1) + (v2^(2)-v1^(2))/(2*a2)=51004.5m`

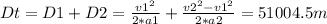
Step-by-step explanation:

For any movement with constant acceleration:

Vf = vo + a*Δt. Replacing the propper values, with get the answers for parts a) and b):

v1 = a1*t1 = 2162 m/s

v2 = v1 + a2*(t2-t1) = 2591 m/s

Using the formula for displacement we can calculate the total distance asked on part c):

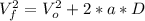`V_(f)^(2)=V_(o)^2+2*a*D` Solving for D and replacing the values for each part of the launch:

`D=(V_(f)^(2)-V_(o)^(2))/(2*a)`

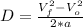
D1 = 24863m

D2 = 26141.5m

Finally we add D1 + D2 for the total distance:

D = 51004.5m