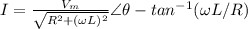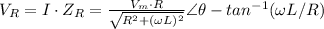Question

A series R-L circuit is given. Circuit is connected to an AC voltage generator. a) Derive equations for magnitude and phase of current and voltages on resistor and inductor in the phasor domain. Assume that the resistance of the resistor is R, inductance of the inductor is L, magnitude of the source voltage is Vm and phase of the source voltage is θ. Note that you don’t have numbers in this step, so to find the magnitude and phase for current I and voltages VR and VL you must first derive both numerator and denominator in polar form using variables R, omega, L, Vm, Vphase (do not use numbers). The solutions should look like equations in slide 24/27! b) In this step, assume that R

Answer 1

The equations for magnitude and phase of current and voltages on resistor and inductor are:

`I=(V_m)/(√(R^2+(\omega L)^2))\angle \theta - tan^(-1)(\omega L / R)`

`V_R=I\cdot Z_R=(V_m \cdot R)/(√(R^2+(\omega L)^2))\angle \theta - tan^(-1)(\omega L / R)`

`V_L=I\cdot Z_L=(V_m \cdot (\omega L))/(√(R^2+(\omega L)^2))\angle \theta - tan^(-1)(\omega L / R)+90^(\circ)`

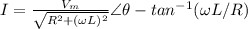
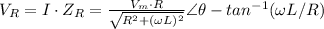
Step-by-step explanation:

The first step is to find the impedances of the resistance (R) and the inductor (L).

The impedance of the resistor is:

• Rectangular form:
  `Z_R=R`
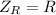
• Polar form:
  `Z_R=R\angle 0^(\circ)`

The impedance of the inductor is:

• Rectangular form:
  `Z_L=j\omega L`

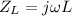
• Polar form:
  `Z_L=\omega L \angle 90^(\circ)`

Where
`\omega` is the angular frequency of the source, and the angle is
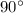`90^(\circ)` because a pure imaginary number is on the imaginary axis (y-axis).

The next step is to find the current expression. It is the same for the resistor and inductor because they are in series. The total impedance equals the sum of each one.

`I=(V)/(Z_R+Z_L)`

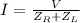
It is said that
`V=V_m\angle \theta`, so, the current would be:

`I=(V_m\angle \theta )/(R+j\omega L)`

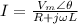
The numerator must be converted to polar form by calculating the magnitude and the angle:

• The magnitude is
  `√(R^2+(\omega L)^2)`
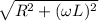
• The angle is
  `tan^(-1)(\omega L / R)`

The current expression would be as follows:

`I=(V_m\angle \theta )/(√(R^2+(\omega L)^2)\, \angle tan^(-1)(\omega L / R))`

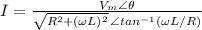
When dividing, the angles are subtracted from each other.

The final current expression is:

`I=(V_m)/(√(R^2+(\omega L)^2))\angle \theta - tan^(-1)(\omega L / R)`

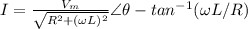
The last step is calculating the voltage on the resistor
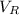`V_R` and the voltage on the inductor
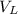`V_L`. In this step the polar form of the impedances could be used. Remember that
`V=I\cdot Z`.

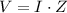(Also remember that when multiplying, the angles are added from each other)

Voltage on the resistor
`V_R`

`V_R=I\cdot Z_R=\bigg( (V_m)/(√(R^2+(\omega L)^2))\angle \theta - tan^(-1)(\omega L / R)\bigg) \cdot (R\angle 0^(\circ))`

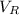
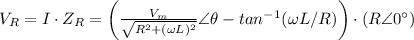
The final resistor voltage expression is:

`V_R=I\cdot Z_R=(V_m \cdot R)/(√(R^2+(\omega L)^2))\angle \theta - tan^(-1)(\omega L / R)`

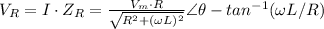
Voltage on the inductor
`V_L`

`V_L=I\cdot Z_L=\bigg( (V_m)/(√(R^2+(\omega L)^2))\angle \theta - tan^(-1)(\omega L / R)\bigg) \cdot (\omega L \angle 90^(\circ))`

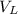
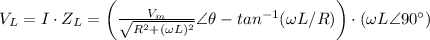
The final inductor voltage expression is:

`V_L=I\cdot Z_L=(V_m \cdot (\omega L))/(√(R^2+(\omega L)^2))\angle \theta - tan^(-1)(\omega L / R)+90^(\circ)`

Summary: the final equations for magnitude and phase of current and voltages on resistor and inductor are:

`I=(V_m)/(√(R^2+(\omega L)^2))\angle \theta - tan^(-1)(\omega L / R)`

`V_R=I\cdot Z_R=(V_m \cdot R)/(√(R^2+(\omega L)^2))\angle \theta - tan^(-1)(\omega L / R)`

`V_L=I\cdot Z_L=(V_m \cdot (\omega L))/(√(R^2+(\omega L)^2))\angle \theta - tan^(-1)(\omega L / R)+90^(\circ)`