Question

Two small particles of mass m1 and mass m2 attract each other with a force that varies inversely with the cube of their separation. At time t0,m1 has a velocity of magnitude v0, directed towards m2, which is at rest a distance d away. At time t1, the particles collide. Calculate L, the distance traveled by particle 1 during the time interval t1 − t0. Express your answer using some or all of the following variables: m1, m2, t0, t1, v0, and d.

Answer 1

`r_(cm)\ =\ (m_2d\ +\ m_1v_0 (t_1\ -\ t_0))/(m_1\ +\ m_2)`

Step-by-step explanation:

Given,

• mass of the first particle =
  `m_1`
• velocity of the first particle =
  `v_o`
• mass of the second particle =
  `m_2`
• velocity of the second particle =
  `v_2 = 0`
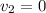
• Time interval =
  `(t_1\ -\ t_o)`

Let
`v_(cm)` be the initial velocity of the center of mass of the system of particle at time
`t_o`

`\therefore v_(cm)\ =\ (m_1v_1\ +\ m_2v_2)/(m_1\ +\ m_2)\\\Rightarrow v_(cm)\ =\ (m_1v_0)/(m_1\ +\ m_2)`

Assuming that the first particle is at origin, distance of the second particle from the origin is 'd'

• 
  `x_1\ =\ 0`
• 
  `x_2\ =\ d`

Center of mass of the system of particles

`x_(cm)\ =\ (m_1x_1\ +\ m_2x_2)/(m_1\ +\ m_2)\\\Rightarrow x_(cm)\ =\ (m_2d)/(m_1\ +\ m_2)\\`

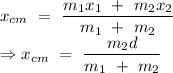
Hence, at time
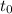`t_0`, the center of mass of the system is at
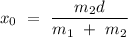`x_0\ =\ (m_2d)/(m_1\ +\ m_2)` at an initial speed of
`v_(cm)`

Both the particles are assumed to be the point masses, therefore at the time
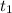`t_1` the center of mass is at the position of the second particle which should be equal to the total distance traveled by the first particle because the second particle is at rest.

Let
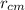`r_(cm)` be the distance traveled by the center of mass of the system of particles in the time interval
`(t_1\ +\ t_0)`

From the kinematics,

`s\ =\ x_0\ +\ vt\\\Rightarrow r_(cm)\ =\ x_(cm)\ +\ v_(cm){t_1\ -\ t_0}\\\Rightarrow r_(cm)\ =\ (m_2d)/(m_1\ +\ m_2)\ +\ \left ( (m_1v_0)/(m_1\ +\ m_2)\ \right )* (t_1\ -\ t_0)\\\Rightarow r_(cm)\ =\ (m_2d\ +\ m_1v_0 (t_1\ -\ t_0))/(m_1\ +\ m_2)`

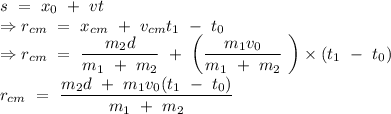
Hence, this is the required distance traveled by the first mass to collide with the second mass which is at rest.