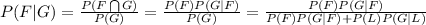Answer:
the probability that the user is fraudulent is 0.00299133
Explanation:
Let be the events be:
G: The user generates calls from two or more areas.
NG: The user does NOT generate calls from two or more areas.
L: The user is legitimate.
F: The user is fraudulent.
The probabilities established in the statement are:
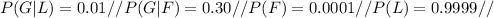
With these values, the probability that a user is fraudulent, if it has originated calls from two or more areas is: