Question

Preliminary data analyses indicate that it is reasonable to use a t-test to carry out the specified hypothesis test. Perform the t-test. Be sure to state the hypotheses and the P-Value. State your conclusion in a sentence. A test of sobriety involves measuring a subject's motor skills. The mean score for men who are sober is known to be 35.0. A researcher would like to perform a hypothesis test to determine whether the mean score for sober women differs from 35.0. Twenty randomly selected sober women take the test and produce a mean score of 41.0 with a standard deviation of 3.7. Perform the hypothesis test at the 0.01 level of significance.

Answer 1

Answer with explanation:

By considering the given information, we have

Null hypothesis :
`H_0: \mu=35.0`

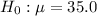
Alternative hypothesis :
`H_1: \mu\\eq35.0`

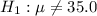
Since the alternative hypothesis is two-tailed , so the test is a two-tailed test.

Given : Sample size : n= 20, since sample size is less than 30 so the test applied is a t-test.

`\overline{x}=41.0` ;
`\sigma= 3.7`

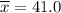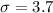
Test statistic :
`t=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}`

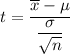
i.e.
`t=(41.0-35.0)/((3.7)/(√(20)))=7.252112359\approx7.25`

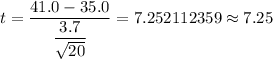
Degree of freedom : n-1 = 20-1=19

Significance level = 0.01

For two tailed, Significance level
`=(0.01)/(2)=0.005`

By using the t-distribution table, the critical value of t =
`t_(19, 0.005)=2.861`

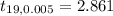
Since , the observed t-value (7.25) is greater than the critical value (2.861) .

So we reject the null hypothesis, it means we have enough evidence to support the alternative hypothesis.

We conclude that there is some significance difference between the mean score for sober women and 35.0.