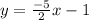Question

What is the equation of the line that is parallel to the line 5x + 2y = 12 and passes through the point (−2, 4)? y = – Five-halvesx – 1 y = – Five-halvesx + 5 y = Two-fifthsx – 1 y = Two-fifthsx + 5

Answer 1

Answer is A

Explanation:

Trust the process

Answer 2

`y= (-5)/(2)x-1`

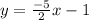
Explanation:

the line equation is 5x + 2y = 12

Solve for y to find out slope m

y=mx+b

`5x + 2y = 12`

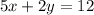
Subtract 5x from both sides

`2y =-5x+12`

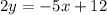
Divide both sides by 2

`y=(-5)/(2) x+6`

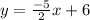
slope = -5/2

Slope of parallel lines are same . So slope of parallel line is
`(-5)/(2)`

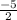
m=-5/2 , point (-2,4)

`y-y_1= m(x-x_1)`

`y-4= (-5)/(2)(x+2)`

`y-4= (-5)/(2)x-5`

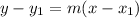
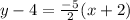
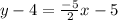
Add 4 on both sides

`y= (-5)/(2)x-1`