Question

When M2S3(s) is heated in air, it is converted to MO2(s). A 3.280 g sample of M2S3(s) shows a decrease in mass of 0.228 g when it is heated in air. What is the average atomic mass of M?

Answer 1

The average atomic mass of M is 181.33 g/mol.

Step-by-step explanation:

First off we need to know the reaction that takes place. The balanced reaction of M₂S₃(s) is:

• M₂S₃(s) + O₂(g) ⇒2MO₂(s) + 3SO₂(g)

The important section for this problem is this:

• M₂S₃(s) ⇒2MO₂(s)

**Thus, the number of moles of M in M₂S₃ is equal to the number of moles of M in 2MO₂.

The decrease in mass means that M₂S₃ reacted and produced MO₂, thus the mass of MO₂ is 3.280-0.228=3.052 g

Now let's say x is the atomic weight of M, and write the molecular weights (Mw) of those two compounds:

Mw of M₂S₃= 2x + 96 g/mol

Mw of MO₂= x + 32 g/mol

Now we determine the moles of each compound, using the formula [ moles = mass / molecular weight ]:

Moles of M₂S₃=
`(3.280g)/(2x+96g/mol)`

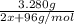
Moles of MO₂=
`(3.052g)/(x+32g/mol)`

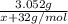
Using the equivalence marked by asterisks, we're left with (note that the second denominator is multiplied by 2 because of the reaction coefficients):

`(3.280g)/(2x+96g/mol)=(3.052g)/(2x+64g/mol)`

We solve for x:

}[/tex]

Thus, the average atomic mass of M is 181.33 g/mol.