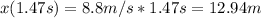Question

A worker on the roof of a house drops his 0.46 kg hammer, which slides down the roof at constant speed of 9.88 m/s. The roof makes an angle of 27 ◦ with the horizontal, and its lowest point is 17.1 m from the ground. what is the the horizontal distance traveled by the hammer between the time is leaves the roof of the house and the time it hits the ground?

Answer 1

The horizontal distance travelled in that time lapse is 12.94 m

Step-by-step explanation:

In order to solve this problem, we'll need:

1. The horizontal speed
2. the time the hammer takes to fall from the roof to the ground

At the lowest point of the roof, the hammer has a 9.88 m/s speed that makes an angle of 27° with the horizontal, so we can calculate the horizontal and vertical speed with trigonometry. If we take right as x positive and down as y positive we get

`v_(x)=v*cos(27)=9.88 m/s *cos(27)=8.80 m/s \\v_(y)=v*sen(27)=9.88 m/s *sen(27)=4.49 m/s`

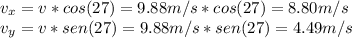
Now, we make two movement equation as we have a URM (no acceleration) in x and an ARM (gravity as acceleration) in y. We will wisely pick the lowest point of the roof as the origin of coordinates

`x(t)=8.8 m/s *t`

`y(t)=4.49m/s*t+(1)/(2)*9.8m/s^(2)*t^(2)`

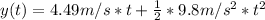
Now we calculate the time the hammer takes to get to the floor

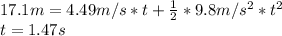`17.1m=4.49m/s*t+(1)/(2)*9.8m/s^(2)*t^(2)\\t=1.47s` or
`t=-2.38s`

Now, we keep the positive time result and calculate the horizontal distance travelled

`x(1.47s)=8.8m/s*1.47s=12.94m`