Answer:
Ans. B) 22 m/s (the closest to what I have which was 20.16 m/s)
Step-by-step explanation:
Hi, well, first, we have to find the equations for both, the driver and the van. The first one is moving with constant acceleration (a=-2m/s^2) and the van has no acceletation. Let´s write down both formulas so we can solve this problem.
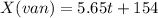
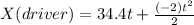
or by rearanging the drivers equation.

Now that we have this, let´s equal both equations so we can tell the moment in which both cars crashed.
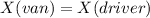
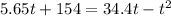
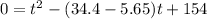

To solve this equation we use the following formulas
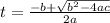
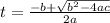
Where a=1; b=-28.75; c=154
So we get:
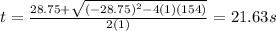
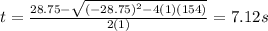
At this point, both answers could seem possible, but let´s find the speed of the driver and see if one of them seems ilogic.
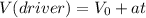 }
}
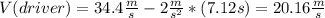
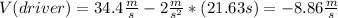
This means that 21.63s will outcome into a negative speed, for that reason we will not use the value of 21.63s, we use 7.12s and if so, the speed of the driver when he/she hits the van is 20.16m/s, which is closer to answer A).
Best of luck