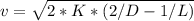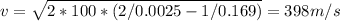Answer:
398 m/s
Step-by-step explanation:
The acceleration is given by:
a = K/(L - x)^2
K = 100 m^3/s^2
L = 0.169 m
This acceleration will result in a force:
F = m * a
F = m * K/(L - x)^2
This force will perform a work:
W = F * L
The ball will advance only until x = L - D/2
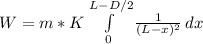
This work will be converted to kinetic energy
W = Ek
Ek = 1/2 * m * v^2
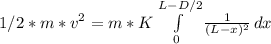

First we solve thr integral:
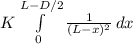
We use the replacement
u = L - x
du = -dx
And the limits
When x = L - D/2, u = D2/2, and when x = 0, u = L
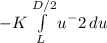
K / u evaluated between L and D/2
2*K / D - K / L
Then
1/2 * v^2 = 2*K / D - K / L
1/2 * v^2 = K * (2/D - 1/L)
v^2 = 2*K*(2/D - 1/L)