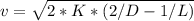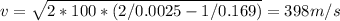Question

The steel ball A of diameter D = 25 mm slides freely on the horizontal rod of length L = 169 mm which leads to the pole face of the electromagnet. The force of attraction obeys an inverse-square law, and the resulting acceleration of the ball is a = K/(L - x)2, where K = 100 m3/s2 is a measure of the strength of the magnetic field. If the ball is released from rest at x = 0, determine the velocity v with which it strikes the pole face.

Answer 1

398 m/s

Step-by-step explanation:

The acceleration is given by:

a = K/(L - x)^2

K = 100 m^3/s^2

L = 0.169 m

This acceleration will result in a force:

F = m * a

F = m * K/(L - x)^2

This force will perform a work:

W = F * L

The ball will advance only until x = L - D/2

`W = m * K \int\limits^(L - D/2)_0 {(1)/((L - x)^2)} \, dx`

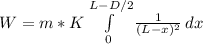
This work will be converted to kinetic energy

W = Ek

Ek = 1/2 * m * v^2

`1/2 * m * v^2 = m * K \int\limits^(L - D/2)_0 {(1)/((L - x)^2)} \, dx`

`1/2 * v^2 = K \int\limits^(L - D/2)_0 {(1)/((L - x)^2)} \, dx`

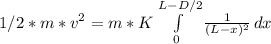
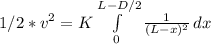
First we solve thr integral:

`K \int\limits^(L - D/2)_0 {(1)/((L - x)^2)} \, dx`

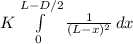
We use the replacement

u = L - x

du = -dx

And the limits

When x = L - D/2, u = D2/2, and when x = 0, u = L

`-K \int\limits^(D/2)_L {u^-2}} \, du`

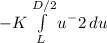
K / u evaluated between L and D/2

2*K / D - K / L

Then

1/2 * v^2 = 2*K / D - K / L

1/2 * v^2 = K * (2/D - 1/L)

v^2 = 2*K*(2/D - 1/L)

`v = √(2*K*(2/D - 1/L))`

`v = √(2*100*(2/0.0025 - 1/0.169)) = 398 m/s`