Answer:
31.75 m/s
Step-by-step explanation:
h = 41.7 m
Let the initial velocity of the second stone is u
Let the time taken to reach to the bottom by the first stone is t then the time taken by the second stone to reach the ground is t - 1.8.
For first stone:
Use second equation of motion
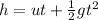
Here, u = 0, g = 9.8 m/s^2 and t be the time and h = 41.7
So, 41.7= 0 + 0.5 x 9.8 x t^2
41.7 = 4.9 t^2
t = 2.92 s ..... (1)
For second stone:
Use second equation of motion
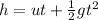
Here, g = 9.8 m/s^2 and time taken is t - 1.8 = 2.92 - 1.8 = 1.12 s, h = 41.7 m and u be the initial velocity
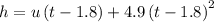 .... (2)
.... (2)
By equation the equation (1) and (2), we get

u = 31.75 m/s