Question

If 3x-y=123x−y=123, x, minus, y, equals, 12, what is the value of \dfrac{8^x}{2^y} 2 y 8 x ​ start fraction, 8, start superscript, x, end superscript, divided by, 2, start superscript, y, end superscript, end fraction ?

Answer 1

The value of the expression
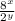`\((8^x)/(2^y)\)` given the equation 3x - y = 12 is 4096, since 8 can be expressed as 2^3 and the properties of exponents allow us to simplify the expression to 2^12.

Step-by-step explanation:

The question involves determining the value of a mathematical expression given a specific equation.

Given the equation 3x - y = 12, we want to find the value of
`\((8^x)/(2^y)\)`.

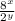This can be done by recognizing that 8 is a power of 2, specifically 8 = 2^3.

Thus,
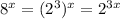`\(8^x = (2^3)^x = 2^(3x)\)`. Substituting back into the original expression, we get
`\((2^(3x))/(2^y)\)`.

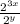Using the properties of exponents, when dividing terms with the same base, we subtract the exponents:
`\(2^(3x - y)\)`.

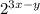Since we know 3x - y = 12, we substitute 12 in place of 3x - y, giving us 2^12.

Therefore, the answer is 2^{12}, or 4096.

Answer 2

`2^(12)=4,096`

Step-by-step explanation:

You know that
`3x-y=12` and have to find

`(8^x)/(2^y)`

Use the main properties of exponents:

1.
`(a^m)^n=a^(m\cdot n)`

2.
`(a^m)/(a^n)=a^(m-n)`

Note that

`8=2^3,`

then

`7^x=(2^3)^x=2^(3\cdot x)=2^(3x)`

Now

`(8^x)/(2^y)=(2^(3x))/(2^y)=2^(3x-y)`

Since
`3x-y=12,` then
`2^(3x-y)=2^(12)=4,096`