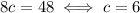The two pieces are continuous for every
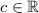
So, our only concern is to make sure that the pieces "glue" continuously at x=7.
To ensure this, we evaluate both pieces at x=7, and impose that the two values are equal.
The first piece evaluates to

The second piece evaluates to
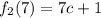
So, we want
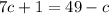
We move all terms involving c to the left hand side, and all the numerical constants on the right hand side: