Question

This is a question for my Calc 1 class at ASU.

Answer 1

90% of people marry there 7th grade love. since u have read this, u will be told good news tonight. if u don't pass this on nine comments your worst week starts now this isn't fake. apparently if u copy and paste this on ten comments in the next ten minutes you will have the best day of your life tomorrow. you will either get kissed or asked out in the next 53 minutes someone will say i love you

Explanation:

Answer 2

The two pieces are continuous for every
`c \in \mathbb{R}`

So, our only concern is to make sure that the pieces "glue" continuously at x=7.

To ensure this, we evaluate both pieces at x=7, and impose that the two values are equal.

The first piece evaluates to

`f_1(7)=7^2-c = 49-c`

The second piece evaluates to

`f_2(7)=7c+1`

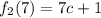
So, we want

`7c+1=49-c`

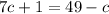
We move all terms involving c to the left hand side, and all the numerical constants on the right hand side:

`8c=48 \iff c=6`