Answer:
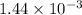 N
N
Step-by-step explanation:
We are given that three charged particle are placed at each corner of equilateral triangle.
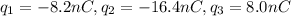


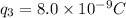
Side of equilateral triangle =3.3 cm=

We know that each angle of equilateral angle=
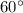
Net force=F =
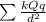
Where k=

If we bisect the angle at
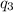 then we have 30 degrees from there to either charge.
then we have 30 degrees from there to either charge.
Direction of vertical force due to charge
 and
and
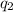
Therefore, force will be added
Vertical force=
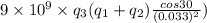
Vertical net force=
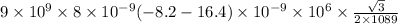
Vertical force =
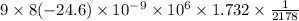
Vertical force=
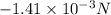 (towards
(towards
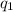
Horizontal component are opposite in direction then will b subtracted
Horizontal force=
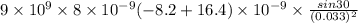
Horizontal force=
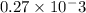 N(towards
N(towards
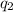
Net electric force acting on particle 3 due to particle =
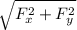
Net force=
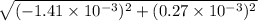
Net force=
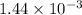 N
N