Question

In an oscillating LC circuit, L ! 25.0 mH and C ! 7.80 mF. At time t 0 the current is 9.20 mA, the charge on the capacitor is 3.80 mC, and the capacitor is charging.What are (a) the total energy in the circuit, (b) the maximum charge on the capacitor, and (c) the maximum current? (d) If the charge on the capacitor is given by q ! Q cos(vt $ f), what is the phase angle f? (e) Suppose the data are the same, except that the capacitor is discharging at t ! 0.What then is f?

Answer 1

a) 926 μJ

b) 3.802 mC

c) 8.61 A

d) 0.0721

e) 3.2137

Step-by-step explanation:

The energy in the inductor is

`El = (1)/(2)*L*I^2`

`El = (1)/(2)*25*10^(-3)*(9.2*10^(-3))^2 = 1.06*10^(-6) J = 1.06 \mu J`

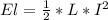
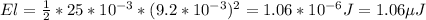
The energy store in a capacitor is

`Ec = (1)/(2)*C*V^2`

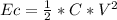
The voltage in a capacitor is

V = Q/C

`V = (3.8*10^(-3))/(7.8*10^(-3)) = 0.487 V`

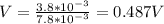
Therefore:

`Ec = (1)/(2)*7.8*10^(-3)*0.487^2 = 9.256*10^(-4) J = 925.6 \mu J`

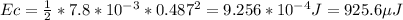
The total energy is Et = 925.6 + 1.1 = 926.7 μJ

At a certain point all the energy of the circuit will be in the capacitor, at this point it will have maximum charge

`Ec = (1)/(2)*C*V^2`

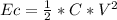
V = Q/C

`Ec = (1)/(2)*C*((Q)/(C))^2`

`Ec = (1)/(2)*(Q^2)/(C)`

`Q^2 = 2*Ec*C`

`Q = √(2*Ec*C)`

`Q = \sqrt{2*926*10{-6}*7.8*10^(-3)} = 3.802 * 10{-3} C = 3.802 mC`

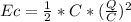
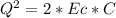
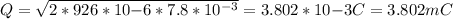
When the capacitor is completely empty all the energy will be in the inductor and current will be maximum

`El = (1)/(2)*L*I^2`

`I^2 = 2*(El)/(L)`

`I = \sqrt{2*(El)/(L)}`

`I = \sqrt{2*(926.7*10^(-3))/(25*10^(-3))} = 8.61 A`

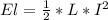
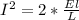
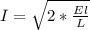
At t = 0 the capacitor has a charge of 3.8 mC, the maximum charge is 3.81 mC

q = Q * cos(vt + f)

q(0) = Q * cos(v*0 + f)

3.8 = 3.81 * cos(f)

cos(f) = 3.8/3.81

f = arccos(3.8/3.81) = 0.0721

If the capacitor is discharging it is a half cycle away, so f' = f + π = 3.2137