Answer:
(a) P( A ∩ B )=0.5 is not possible.
(b) 0.7
(c) 0.3
(d) 0.3
(e) 0.4
Explanation:
Given information: The alphabet A and B represents the following events
A : Individual has a Visa credit card.
B: Individual has a MasterCard.
P(A)= 0.6 and P(B)=0.4.
(a)
We need to check whether P( A ∩ B ) can be 0.5 or not.
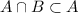 and
and
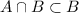
 and
and
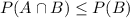
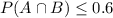 and
and
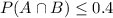
From these two inequalities we conclude that
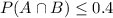
Therefore, P( A ∩ B )=0.5 is not possible.
(b)
Let
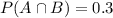
We need to find the probability that student has one of these two types of cards.
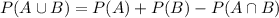
Substitute the given values.
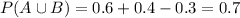
Therefore the probability that student has one of these two types of cards is 0.7.
(c)
We need to find the probability that the selected student has neither type of card.

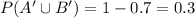
Therefore the probability that the selected student has neither type of card is 0.3.
(d)
The event that the select student has a visa card, but not a mastercard is defined as
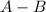
It can also written as

The probability of this event is
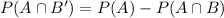
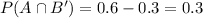
Therefore the probability that the select student has a visa card, but not a mastercard is 0.3.
(e)
We need to find the probability that the selected student has exactly one of the two types of cards.
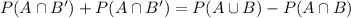
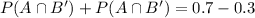

Therefore the probability that the selected student has exactly one of the two types of cards is 0.4.