Question

A student at the top of building of height h throws one ball upward with the initial speed V and then throws a second ball downward with the same initial speed. How do the final speeds of the balls compare when they reach the ground?

Answer 1

Velocity is same

Step-by-step explanation:

Case I:

When the ball throws upwards

Let the velocity of the ball as it hits the ground is V'.

Initial velocity, u = V

Final velocity, v = V'

height = h

acceleration due to gravity = g

Use third equation of motion

`v^(2)=u^(2)+2as`

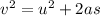
By substituting the values

`V'^(2)=V^(2)+2(-g)(-h)`

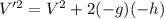
`V'=\sqrt{V^(2)+2gh}` .... (1)

Case II:

When the ball throws downwards

Let the velocity of the ball as it hits the ground is V''.

Initial velocity, u = V

Final velocity, v = V''

height = h

acceleration due to gravity = g

Use third equation of motion

`v^(2)=u^(2)+2as`

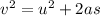
By substituting the values

`V''^(2)=V^(2)+2(-g)(-h)`

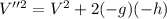
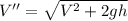`V''=\sqrt{V^(2)+2gh}` .... (2)

By comparing the equation (1) and equation (2), we get

V' = V''

Thus, the velocity of balls in both the cases is same as they strikes the ground.

Answer 2

They are the same (assuming there is no air friction)

Step-by-step explanation:

Take a look at the picture.

When the first ball (the one thrown upward) gets to the point marked as A, the speed will has the exact same value V but the velocity will now point downward (just like the second ball).

So if you think about it, the first ball, from point A to the ground, will behave exactly like the second ball (same initial speed, same height).

That is why the speeds will be the same when they reach the ground.