Answer:
The vector direction is 83.0° relative to the positive x-axis
Explanation:
* Lets explain how to find the direction of a vector
- A vector is a quantity which has both magnitude and direction
- The vector has two components x-component and y-component
- The x-component = v cos Ф , and the y-component = v sin Ф,
where Ф is the angle between the vector and the positive part
of the x-axis
- The magnitude of the vector =
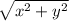
- The direction of the vector =
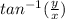
* Lets solve the problem
∵ x-component of the vector = 0.15
∵ y-component of the vector = 1.22
- Both x-component and y-component are positive
∴ Ф will be between 0° and 90°
∵ The direction of the vector =
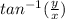
∴ The direction of the vector =
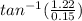
∴ The direction of the vector = 83.0°
* The vector direction is 83.0° relative to the positive x-axis