If the
 and
and
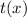 are even function then
are even function then
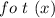 is an even function, if
is an even function, if
 and
and
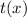 are odd function then the function
are odd function then the function
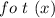 is an odd function and if
is an odd function and if
 is even and
is even and
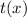 is odd then the function
is odd then the function
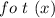 is an even function.
is an even function.
Further explanation:
An even functrion satisfies the property as shown below:
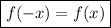
An odd functrion satisfies the property as shown below:

Consider the given composite function as follows:

If both the function
 and
and
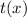 are even function.
are even function.
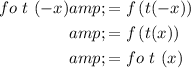
From the above calculation it is concluded that,
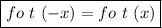
This implies that the composite function
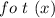 is an even function.
is an even function.
If both the function
 and
and
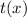 are odd function.
are odd function.

From the above calculation it is concluded that,
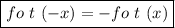
This implies that the composite function
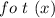 is an odd function.
is an odd function.
If the function
 is even and
is even and
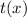 is odd.
is odd.
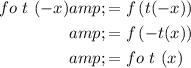
From the above calculation it is concluded that,
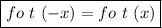
This implies that the composite function
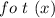 is an even function.
is an even function.