Explanation:
By the problem we know that our events are:
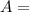 A batch is formed from two different lots.
A batch is formed from two different lots.
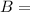 A batch requires additional processing.
A batch requires additional processing.
So, according to that:
a)
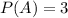
Because P(A) and
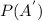 are complementary events
are complementary events
b)

Because of the problem, we know that:
c)
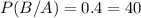
and,
d)
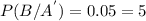
From the formula
e) P(A ∩ B)= P(A)*P(B/A)=

f) P(A ∩ B')=P(A)-P(A ∩ B)=
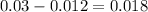
And, finally
g) P(B)=P(B/A)*P(A)+P(B/A')*P(A')=
