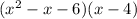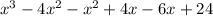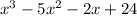Answer:
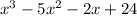
Explanation:
the polynomial function of least degree whose only zeros are -2, 3, and 4
Factors are -2,3 and 4
First we write the polynomial in factor form
If 'a' is a zero of the polynomial then (x-a) is a factor
Factors are -2,3 and 4
Polynomial is
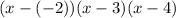

Now we multiply all the parenthesis