Question

A 2D vector can have a component equal to zero even when its magnitude is nonzero.

The direction of a vector can be different in different coordinate systems.
A 2D vector can have a magnitude equal to zero even when one of its components it nonzero.
The magnitude of a vector can be different in different coordinate systems.
It is possible to multiply a vector by a scalar. It is possible to add a scalar to a vector.
The components of a vector can be different in different coordinate systems.

True or False

Answer 1

T F F F T F T

Explanation:

A 2D vector can have a component equal to zero even when its magnitude is nonzero. TRUE.

it will be actually a 1d vector, but it's still a 2d vector too. this happens when the vector it's aligned to one of the axis.

The direction of a vector can be different in different coordinate systems. FALSE

The direction of a vector is independent of any coordinate system.

A 2D vector can have a magnitude equal to zero even when one of its components it nonzero. FALSE.

because the only way
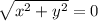`\sqrt{x^(2) +y^(2) } =0` is that both x and y are equal to zero

The magnitude of a vector can be different in different coordinate systems. FALSE.

The magnitude stays the same in every coordinate system

It is possible to multiply a vector by a scalar. TRUE.

it changes only it's magnitude.

It is possible to add a scalar to a vector. FALSE.

you can´t sum elements of diferent spaces. R,
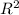`R^(2)`, etc

The components of a vector can be different in different coordinate systems.TRUE.

The components of a vector are just a way for identifying the vector, in a determinate coordinate system, the way i call those components will change as I change the name I call every point in the plane.