Loren drove 200 miles at a certain rate, and his wife, Lois, drove 100 miles at a rate 10 mph slower. If Loren had driven for the entire trip, they would have arrived 30 minutes…

Question

asked May 14, 2020 103k views

2 Answers

Erik Vullings · Answer 1 · 2020-05-20T21:35:21+0000

As long as Loren drove, the law of motion was

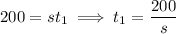
$200 = st_1 \implies t_1 = (200)/(s)$

As long as Loid drove, the law of motion was

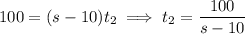
$100 = (s-10)t_2 \implies t_2 = (100)/(s-10)$

So, the total time they took is

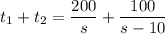
t_1+t_2=(200)/(s)+(100)/(s-10)

Had Loren driven the whole time, the law of motion would have been

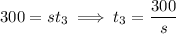
$300=st_3 \implies t_3 = (300)/(s)$

And we know that this time would have been 30 minutes (i.e. 0.5 hours) faster. So, we have

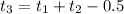
t_3 = t_1+t_2-0.5

This translates into

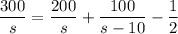
(300)/(s)=(200)/(s)+(100)/(s-10)-(1)/(2)

If we subtract 200/s from both sides, we have

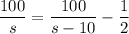
(100)/(s)=(100)/(s-10)-(1)/(2)

We can simplify the right hand side by summing the two fractions:

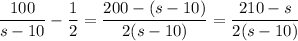
(100)/(s-10)-(1)/(2) = (200-(s-10))/(2(s-10))=(210-s)/(2(s-10))

So, we have to solve

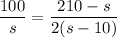
(100)/(s)=(210-s)/(2(s-10))

If we cross multiply the denominators, we have

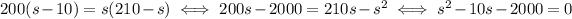
$200(s-10)=s(210-s) \iff 200s-2000=210s-s^2 \iff s^2-10s-2000=0$

Which yields the solutions

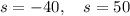
$s=-40,\quad s=50$

We accept the positive solution, because the negative would mean to travel backwards, so Loren's rate was 50mph