Answer: The correct options are
(1) C. The graphs are identical.
(2) B. g(x) = (x + 7)² - 5
Step-by-step explanation:
(1) We are to find the relation between the graphs of the functions y = f(x) and y = f(–x) when
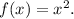
We have

Since both the functions are same, so the graphs of y = f(x) and y = f(–x) are identical.
Option (C) is CORRECT.
(2) We are to write equation of the function g(x) that translates the parent function f(x) = x² by shifting g(x) 7 units to the left and 5 units down.
We know that
if a function y = f(x) is shifted a units to the left and 5 units down, then the new function is given by
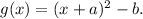
For the given translation, a = 7 and b = 5.
Therefore, the new function is given by
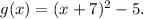
Thus, option (B) is CORRECT.