Question

HELP PLEASE !!29. How do the graphs of the functions y = f(x) and y = f(–x) relate when

f(x) = x2 ?


A.The graphs reflect each other.

B.The second graph is a horizontal shift of the first graph by x units.

C.The graphs are identical.

D.The second graph is a vertical shift of the first graph by x units.



30. Write the equation of the function g(x) that translates the parent function

f(x) = x² by shifting g(x) 7 units to the left and 5 units down.


A. g(x) = (x - 7)² - 5

B. g(x) = (x + 7)² - 5

C. g(x) = (x - 5)² - 7

D. g(x) = (x + 5)² - 7

Answer 1

29. The graphs reflect each other.

30. g(x)=(x+7)^2 -5

Explanation:

Answer 2

Answer: The correct options are

(1) C. The graphs are identical.

(2) B. g(x) = (x + 7)² - 5

Step-by-step explanation:

(1) We are to find the relation between the graphs of the functions y = f(x) and y = f(–x) when

`f(x)=x^2.`

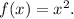
We have

`y=f(x)=x^2,\\\\y=f(-x)=(-x)^2=x^2.`

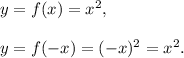
Since both the functions are same, so the graphs of y = f(x) and y = f(–x) are identical.

Option (C) is CORRECT.

(2) We are to write equation of the function g(x) that translates the parent function f(x) = x² by shifting g(x) 7 units to the left and 5 units down.

We know that

if a function y = f(x) is shifted a units to the left and 5 units down, then the new function is given by

`g(x)=(x+a)^2-b.`

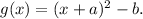
For the given translation, a = 7 and b = 5.

Therefore, the new function is given by

`g(x)=(x+7)^2-5.`

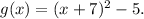
Thus, option (B) is CORRECT.