Answer:
Part 1)
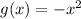
Part 2)
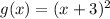
Part 3)

Explanation:
we have
The parent function is
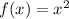
This is a vertical parabola open upward with vertex at origin (0,0)
Part 1) Reflection over the x-axis
The rule of the reflection across the x=axis is equal to
(x,y) ------> (x,-y)
so
f(x) -----> g(x)
The function g(x) will be
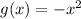
Part 2) Horizontal shift left 3 units
The rule of the translation is
(x,y) ------> (x-3,-y)
so
f(x) -----> g(x)
The function g(x) will be
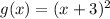
Part 3) Vertical shift up 7 units
The rule of the translation is
(x,y) ------> (x,y+7)
so
f(x) -----> g(x)
The function g(x) will be
