Answer:
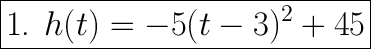

Explanation:
If we're looking for the point at with the ball reaches its highest point, we want to find the graph's vertex. In order to get the equation into a form with the vertex in it, we need to convert the equation into vertex form. This is an equation in the form
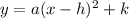 , h being the x value of the vertex, and k being the y value of the vertex.
, h being the x value of the vertex, and k being the y value of the vertex.
In order to convert our equation,
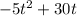 into vertex form, we can algebraically manipulate it to get it into the form we want.
into vertex form, we can algebraically manipulate it to get it into the form we want.
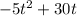
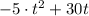 (Separate the -5 from the t^2)
(Separate the -5 from the t^2)
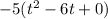 (Factor out a -5)
(Factor out a -5)
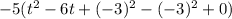 (Completing the Square)
(Completing the Square)
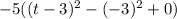 (Binomial Formula)
(Binomial Formula)
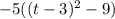 (Simplify)
(Simplify)
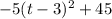 (Factor the -5 back in)
(Factor the -5 back in)
Therefore, our equation with the vertex in it is
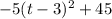 . To find the vertex, we can examine the equation to find the values of h and k in the formula
. To find the vertex, we can examine the equation to find the values of h and k in the formula
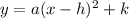 (where the vertex coordinates are (h, k)).
(where the vertex coordinates are (h, k)).
It seems that h is 3 and k is 45. Therefore, the coordinate of the vertex is (3, 45). Since it asks for how many seconds after being hit does the ball reach its highest point, we would take the x value since x represents seconds. This is 3. Therefore, the ball reaches its highest point after 3 seconds.
Hope this helped!