Answer:
Part 1) The end points of the initial incline are the points (0,0) and (4,6)
Par 2) The slope of the initial incline (red) is m=1.5
Part 3) The linear equation of the initial (red ) incline would be y=1.5x
Part 4) The end points of the first decline are the points (4,6) and (6,2)
Part 5) The slope of the first decline (blue) is m=-2
Part 6) The linear equation of the first decline (blue) would be y=-2x+14
Part 7) Two end points of the second incline (green) are the points (6,2) and (10,5)
Part 8) The slope of the second incline (green) is m=0.75
Part 9) The slope of the first decline is the steepest of the three
Part 10) see the explanation
Part 11) The track is not a function
Part 12) see the explanation
Part 13) The domain is all real numbers greater than or equal to 0 and less than or equal to 12
Part 14) The range is all real numbers greater than or equal to 0 and less than or equal to 8
Explanation:
Part 1) Two end points of the initial incline(red) are ( , ) and ( , )
Observing the graph
The end points of the initial incline are the points (0,0) and (4,6)
Part 2) The slope of the initial incline (red) is
we know that
The formula to calculate the slope between two points is equal to
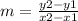
we have
(0,0) and (4,6)
substitute the values in the formula
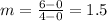
Part 3) The linear equation of the initial (red ) incline would be y = __x +__
we know that
The initial red incline represent a proportional relationship, because is a line that passes through the origin
therefore
The linear equation is
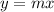
we have
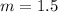
substitute

Part 4) Two end points of the first decline (blue) are ( , ) and ( , )
Observing the graph
The end points of the first decline are the points (4,6) and (6,2)
Part 5) The slope of the first decline (blue) is
we know that
The formula to calculate the slope between two points is equal to
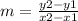
we have
(4,6) and (6,2)
substitute the values in the formula
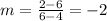
Part 6) The linear equation of the first decline (blue) would be y= __ x + __
The equation of the line in slope intercept form is

we have
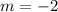
so
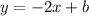
with the point (4,6) find the value of b
substitute the value of x and the value of y in the linear equation
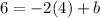
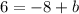
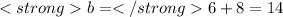
therefore
The linear equation is
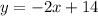
Part 7) Two end points of the second incline (green) are ( , ) and ( , )
Observing the graph
The end points of the second incline are the points (6,2) and (10,5)
Part 8) The slope of the second incline(green) is
we know that
The formula to calculate the slope between two points is equal to
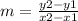
we have
(6,2) and (10,5)
substitute the values in the formula
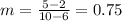
Part 9) Which incline is steepest of the three?
we have
The slope of the initial incline (red) is m=1.5
The slope of the first decline (blue) is m=-2
The slope of the second incline (green) is m=0.75
we know that
The steepest slope is that of the line that is closest to being vertical. This could be a line that has positive slope OR negative slope...the steepest one should be determined by examining the ABSOLUTE VALUES of these three slopes.
This means that the slope of the first decline is the steepest of the three
Part 10) How mathematically can you tell it is the steepest?
we know that
The slope with highest absolute value is the steepest. Positive slope means the function is ascending left to right, negative slope means it is descending left to right.
In this problem
The slope of the first decline is the highest absolute value (absolute value is 2)
Part 11) For the last (orange) section of the track is the track a function
we know that
The vertical line test is a method that is used to determine whether a given relation is a function or not
In this problem the track section does not pass the vertical line test.
therefore
The track is not a function
Part 12) How do you know it is or isn’t a function for this region?
we know that
A function can only have one output, y, for each unique input, x.
In this problem, applying the vertical line test, the vertical line you draw intersects the graph more than once for any value of x, so the graph is not the graph of a function.
Part 13) What is the domain for the roller coaster in total
we know that
The domain is the interval -----> [0,12]
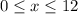
All real numbers greater than or equal to 0 and less than or equal to 12
Part 14) What is the range for the roller coaster in total
we know that
The range is the interval ----> [0,8]
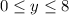
All real numbers greater than or equal to 0 and less than or equal to 8