Question

If x(t) is a solution to the equation x' = f(x), show that x(t + c) is also a solution, for any constant c. Is x(t) + c a solution? Explain why.

Answer 1

Yes, x(t)+C is also a solution of given equation.

Explanation:

We are given that x(t) is a solution of the equation x'=f(x)

We have to show that x(t+c) is also a solution of given equation and check x(t)+c is a solution of equation.

Suppose x'=1

`(dx)/(dt)=1`

`dx=dt`

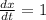
Integrating on both sides

Then , we get

`x=t+c`

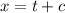
Where C is integration constant.

Now, t replace by t+c

Then, we get

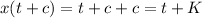`x(t+c)=t+c+c=t+K` because c+C=K

Different w.r.t then we get

`x'=1`

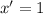
Therefore, x(t+c) is also solution because it satisfied the given equation.

Now, x(t)+C=t+(c+C)=t+L where L=c+C=Constant

Differentiate w.r.t time

Then, we get
`x'=1`

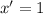
Yes, x(t)+C is also solution of given equation because it satisfied given equation