Question

Simplify each square root expression. Describe the simplified form of the expression as rational or irrational. In your final answer, include all of your work. √121 √48

Answer 1

The Simplified form of
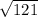`√(121)` is 11, which is a rational number.

The Simplified of
`√(48)` is
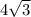`4√(3)` which is an irrational number.

Explanation:

Consider the provided root expression.

Irrational number: A number is irrational if it cannot be expressed by dividing two integers. The decimal expansion of Irrational numbers are neither terminate nor periodic.

Consider the expression
`√(121)`

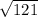
The above expression can be written as:

`\sqrt{11^(2)}=(11^(2))^{(1)/(2)}=(11)^{(2)/(2)}=11`

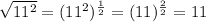
Hence, the Simplified of
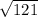`√(121)` is 11, which is a rational number.

Consider the expression
`√(48)`

The above expression can be written as:

`√(48)=\sqrt{4^(2)*3}=4√(3)`

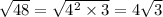
Hence, the Simplified of
`√(48)` is
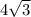`4√(3)` which is an irrational number. Because the decimal expansion of the number is neither terminate nor periodic.

Answer 2

Part 1) 11 is a rational number

Part 2)
`4√(3)` is a irrational number

Explanation:

we know that

A Rational Number is a number that can be made by dividing two integers

Part 1) we have

`√(121)`

we know that

`121=11^(2)`

substitute

`\sqrt{11^(2)}=(11^(2))^{(1)/(2)}=(11)^{(2)/(2)}=11`

Is a rational number, because i can express the number 11 as the ratio of two integers (as example 11/1)

Part 2) we have

`√(48)`

we know that

`48=2^(4)(3)`

substitute

`\sqrt{2^(4)(3)}=(2^(4)(3))^{(1)/(2)}=4√(3)`

Is a irrational number, because cannot be expressed as the ratio of two integers