Question

Suppose you roll a pair of honest dice. If you roll a total of 7 you win $22, if you roll a total of 11 you win $66, if you roll any other total, you lose 911 Find the expected payoff for this game The expected payoff for this game is $ (Round to the nearest cent as needed.)

Answer 1

The expected payoff for this game is -$1.22.

Explanation:

It is given that a pair of honest dice is rolled.

Possible outcomes for a dice = 1,2,3,4,5,6

Two dices are rolled then the total number of outcomes = 6 × 6 = 36.

`\{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),\\(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),\\(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)\}`

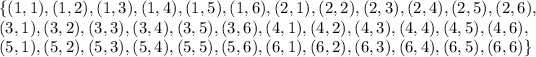
The possible ways of getting a total of 7,

{ (1,6), (2,5), (3,4), (4,3), (5,2), (6,1) }

Number of favorable outcomes = 7

Formula for probability:

`Probability=\frac{\text{Favorable outcomes}}{\text{Total outcomes}}`

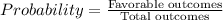
So, the possibility of getting a total of 7 =
`(6)/(36)=(1)/(6)`

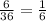
The possible ways of getting a total of 11,

{(5,6), (6,5)}

So, the probability of getting a total of 11 =
`(2)/(36)` =
`(1)/(18)`

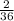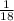
Now, other possible rolls = 36 - 6 - 2 = 36 - 8 = 28,

So, the probability of getting the sum of numbers other than 7 or 11 =
`(28)/(36)` =
`(7)/(9)`

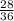Since, for the sum of 7, $ 22 will earn, for the sum of 11, $ 66 will earn while for any other total loss is $11,

Hence, the expected value for this game is

`(1)/(6)* 22+(1)/(18)* 66-(7)/(9)* 11`

`(11)/(3)+(11)/(3)-(77)/(9)`

`(22)/(3)-(77)/(9)`

`(66-77)/(9)`

`-(11)/(9)`

`-1.22`

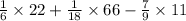
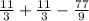
Therefore the expected payoff for this game is -$1.22.