Answer:
a)There is a 0.78% probability of all children being boys.
b) There is a 16.38% probability that there are two girls and five boys.
c) There is a 50% probability that the youngest child is a girl
d) There is a 50% probability that the oldest child is a girl
Explanation:
Probability:
What you want to happen is the desired outcome.
Everything that can happen iis the total outcomes.
The probability is the division of the number of possible outcomes by the number of total outcomes.
In our problem, there is:
-50% probability of giving birth to a boy.
-50% probability of giving birth to a girl.
There are the following babies:
B1 - B2 - B3 - B4 - B5 - B6 - B7
(a) All seven children are boys
For each children there are a 50% probability of it being a boy. So:
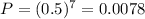
There is a 0.78% probability of all children being boys.
(b) There are two girls and five boys.
There is a 50% probability that each children is a boy and 50% that each children is a girl.
We want five boys and two girls, so we have to permutate these probabilities. It is a permutation of 7 elements(all the children), with 5(boys) and 2(girls) repetitions. So:
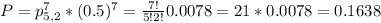
There is a 16.38% that there are two girls and five boys.
(c) The youngest child is a girl
The probabilities are independent, so it is just the probability that B7 is a girl, that is 50%.
(d) The oldest child is a girl
Same as (c), just that the child is B1. The probability of B1 being a girl is 50%.