Question

A small first-aid kit is dropped by a rock climber who is descending steadily at 1.3m/s. After 2.5 s, what is the velocity of the first-aid kit, and how far below the the climber?

Answer 1

1) -25.8 m/s

The velocity of the first-aid kit is given by

`v = u+at`

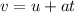
where:

u = -1.3 m/s is the initial velocity (negative because it points downward)

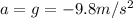`a=g = -9.8 m/s^2` is the acceleration of gravity

t is the time

By substituting t = 2.5 s, we can find the velocity of the kit after 2.5 seconds:

`v=-1.3 + (-9.8)(2.5)=-25.8 m/s`

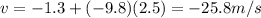
And the negative sign indicates that the velocity of the kit points downward.

2) 30.63 m below

In order to solve this part, we need to calculate the displacement of both the climber and the kit.

The climber descends at constant speed, so his displacement from the starting point is

`d_c = ut`

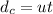
where u = -1.3 m/s. Substituting t = 2.5 s,

`d_c = (-1.3)(2.5 )=-3.25 m`

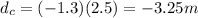
the kit, instead accelerates at a constant rate of
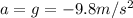`a=g=-9.8 m/s^2`. Therefore, its displacement is given by

`d_k = ut + (1)/(2)at^2`

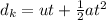
Substituting t = 2.5 s,

`d_k = (-1.3)(2.5) + (1)/(2)(-9.8)(2.5)^2=-33.88 m`

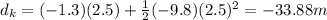
Therefore, the final distance between the kit and the climber is

`d=d_c - d_k = -3.25 m -(-33.88 m)=-30.63 m`

So the kit is 30.63 m below the climber.