1) -25.8 m/s
The velocity of the first-aid kit is given by

where:
u = -1.3 m/s is the initial velocity (negative because it points downward)
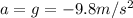 is the acceleration of gravity
is the acceleration of gravity
t is the time
By substituting t = 2.5 s, we can find the velocity of the kit after 2.5 seconds:
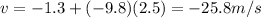
And the negative sign indicates that the velocity of the kit points downward.
2) 30.63 m below
In order to solve this part, we need to calculate the displacement of both the climber and the kit.
The climber descends at constant speed, so his displacement from the starting point is
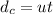
where u = -1.3 m/s. Substituting t = 2.5 s,
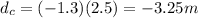
the kit, instead accelerates at a constant rate of
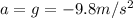 . Therefore, its displacement is given by
. Therefore, its displacement is given by
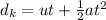
Substituting t = 2.5 s,

Therefore, the final distance between the kit and the climber is

So the kit is 30.63 m below the climber.