Answer: 5.657 units
Explanation:
Given : A crawling insect sits in a 8 x 8 x 8 room. It starts on the center of the floor of the cube.
Since each of the side has equal measure , so it must be a cube.
Also, each face of cube is a square having each angle as right angle.
Then, the dimension of ceiling of room will be 8 x 8 .
Let x be the diagonal of ceiling .
Then By Pythagoras theorem of right angle triangle , we have
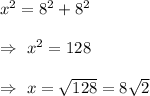
Thus , length of diagonal of ceiling =
 units
units
Also, the diagonals of a square bisect each other, then the distance from center to corner of ceiling = half of diagonal
Then, distance from center to corner of ceiling =

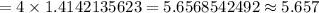
Hence, it must travel to crawl to a corner on the ceiling = 5.657