Question

A crawling insect sits in a 8x8x8 room. It starts on the center of the floor of the cube.

How far must it travel to crawl to a corner on the ceiling? (answer to 3 decimal places)

Answer 1

Answer: 5.657 units

Explanation:

Given : A crawling insect sits in a 8 x 8 x 8 room. It starts on the center of the floor of the cube.

Since each of the side has equal measure , so it must be a cube.

Also, each face of cube is a square having each angle as right angle.

Then, the dimension of ceiling of room will be 8 x 8 .

Let x be the diagonal of ceiling .

Then By Pythagoras theorem of right angle triangle , we have

`x^2=8^2+8^2\\\\\Rightarrow\ x^2=128\\\\\Rightarrow\ x=√(128)=8√(2)`

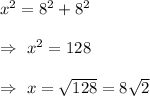
Thus , length of diagonal of ceiling =
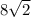`8√(2)` units

Also, the diagonals of a square bisect each other, then the distance from center to corner of ceiling = half of diagonal

Then, distance from center to corner of ceiling =
`(8√(2))/(2)=4√(2)`

`=4*1.4142135623=5.6568542492\approx5.657`

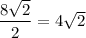
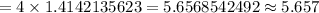
Hence, it must travel to crawl to a corner on the ceiling = 5.657