Answer:
a.0.0078125
b. 0.1640625
c. 0.0078125
d. 0.0078125
Explanation:
To solve this question we can use the binomial probability function:
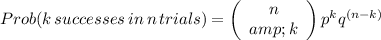
where
- n is the number of trials in this case the number of children
- k is the number of successes, we can think it as the number of boys
- p is the probability that is a boy
- q is the probability that is a girl,
In this case case p=q
Then
(a)
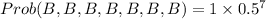
(b)
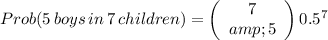
(c)
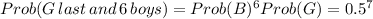
(d)
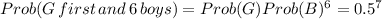
(a), (c) and (d) are equal as a result of equal probability of giving birth to a boy or a girl. (b) is different because it takes into account the different orders that births can occur