Answer:
(a) 5.04 eV (B) 248.14 nm (c)

Step-by-step explanation:
We have given Wavelength of the light \lambda = 240 nm
According to plank's rule ,energy of light
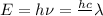
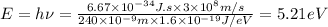
Maximum KE of emitted electron i= 0.17 eV
Part( A) Using Einstien's equation
 , here
, here
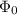 is work function.
is work function.
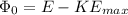 = 5.21 eV-0.17 eV = 5.04 eV
= 5.21 eV-0.17 eV = 5.04 eV
Part( B) We have to find cutoff wavelength
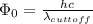
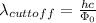
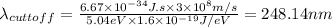
Part (C) In this part we have to find the cutoff frequency
