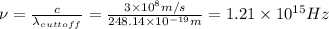Question

When light of wavelength 240 nm falls on a cobalt surface, electrons having a maximum kinetic energy of 0.17 eV are emitted. Find values for the following. (a) the work function of cobalt eV (b) the cutoff wavelength nm (c) the frequency corresponding to the cutoff wavelength Hz

Answer 1

(a) 5.04 eV (B) 248.14 nm (c)
`1.21* 10^(15)Hz`

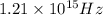
Step-by-step explanation:

We have given Wavelength of the light \lambda = 240 nm

According to plank's rule ,energy of light

`E = h\\u = \frac{hc}{}\lambda`

`E = h\\u = (6.67* 10^(-34) J.s* 3* 10^(8)m/s)/( 240* 10^(-9) m* 1.6* 10^(-19)J/eV)= 5.21 eV`

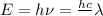
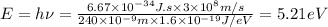
Maximum KE of emitted electron i= 0.17 eV

Part( A) Using Einstien's equation

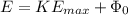`E = KE_(max)+\Phi _(0)`, here
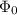`\Phi _0` is work function.

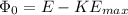`\Phi _(0)=E - KE_(max)`= 5.21 eV-0.17 eV = 5.04 eV

Part( B) We have to find cutoff wavelength

`\Phi _(0) = (hc)/(\lambda_(cuttoff))`

`\lambda_(cuttoff)= (hc)/(\Phi _(0) )`

`\lambda_(cuttoff)= (6.67* 10^(-34) J.s* 3* 10^(8)m/s)/(5.04 eV* 1.6* 10^(-19)J/eV )=248.14 nm`

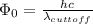
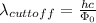
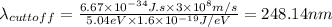
Part (C) In this part we have to find the cutoff frequency

`\\u = (c)/(\lambda_(cuttoff))= (3* 10^(8)m/s)/(248.14 * 10^(-19) m )= 1.21* 10^(15) Hz`