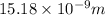Answer:
Step-by-step explanation:
Radius of the path of electron which is moving perpendicular to magnetic field is defined as,
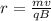
Here, m is the mass of electron, v is the velocity of electron, q is the charge on electron, and B is the magnetic field.
Given that, the velocity of electron is,
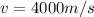 .
.
And the magnetic field is
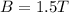 .
.
And the mass of electron is,

And the charge on electron is,
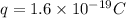
Put all these values in radius equation,
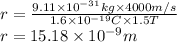
Therefore, the path radius of a moving electron is